Clase # 16 mapas de karnaugh

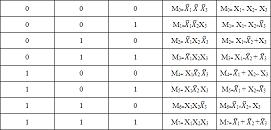
MAPAS DE KARNAUGH

Reglas de simplificación

1.  Las agrupaciones son exclusivamente de unos. Esto implica que ningún grupo puede contener ningún cero.

2. Las agrupaciones únicamente pueden hacerse en horizontal y vertical. Esto implica que las diagonales están prohibidas.

3.  Los grupos han de contener 2ⁿ elementos. Es decir que cada grupo tendrá 1,2,4,8... número de unos.

 

4.  Cada grupo ha de ser tan grande como sea posible. Tal y como lo ilustramos en el ejemplo.

5.  Todos los unos tienen que pertenecer como mínimo a  un grupo. Aunque pueden pertenecer a más de uno.

6.  Pueden existir solapamiento de grupos.

7.  La formación de grupos también se puede producir con las celdas extremas de la tabla. De tal forma que la parte inferior se podría agrupar con la superior y la izquierda con la derecha tal y como se explica en el ejemplo.

8.  Tiene que resultar el menor número de grupos posibles siempre y cuando no contradiga ninguna de las reglas anteriores. Esto es el número de grupos ha de ser minimal.

 

EJERCICIO EN CLASE

 

 

 

 

 

 

 

 

Clase # 15

ACTIVIDAD

Graficar este circuito

 

 

 

Clase #14 tablas deverdad

EJERCICIOS DE TABLAS DE VERDAD

Resolver los siguientes circuitos con tablas de verdad

 

 

Clase # 13 algebra de boogle y mapas de karnaugh

Algebra de Boogle.

Es una rama especial del álgebra que se usa principalmente en electrónica digital. El álgebra booleana fue inventada en el año 1854 por el matemático inglés George Boole.

El álgebra de Boole es un método para simplificar los circuitos lógicos (o a veces llamados circuitos de conmutación lógica) en electrónica digital.

Por lo tanto, también se llama como "Cambio de álgebra". Podemos representar el funcionamiento de los circuitos lógicos utilizando números, siguiendo algunas reglas, que son bien conocidas como "Leyes del álgebra de Boole".

Mapas de karnaugh

Los mapas de Karnaugh constituyen un método sencillo y apropiado para la minimización de funciones lógicas. El tamaño del mapa depende depende del numero de variables, y el método de minimización es efectivo para expresiones de hasta 6 variables.

Representación de funciones con mapas de Karnaugh

Un mapa de Karnaugh es una representación gráfica de una tabla de verdad, y por lo tanto existe una asociación unívoca entre ambas. La tabla de verdad tiene una fila por cada mintérmino, mientras que el mapa de Karnaugh tiene una celda por cada mintérmino. De manera análoga, también existe una correspondencia unívoca entre las filas de la tabla de verdad y las celdas del mapa de Karnaugh si se utilizan maxtérminos

 

 

Clase # 12 compuertas logicas

Compuertas logicas

 

1-v-encendido,  0-f-apagado.

•  AND-Y- ^  

           

 X*Y

 

X  Y    Z

0   0     0

0    1    0

1    0    0

1    1    1

 

• OR-0-V       

 

 

X+Y

X    Y       Z

0     0       0

0     1       1

1     0       1

 1     1       1 

 

• X+R

                 

 

   X     Y      Z  

0      0      0

0      1      1

1       0      1

1       1      0

• NAND

 

X     Y    Z   N.Z

0      0      0      1

0      1      0       1

1      0      0       1

1      1       1     0

 

• Negacion XOR

 

N. X+Y

  X      Y     Z     N.Z

0      0       0      1

0      1       1       0

 1      0      1        0

 1       1       1       0

 

• Negacion de XNOR

 

N.X+Y

X     Y     Z     N.Z

0       0       0       1

0       1       1       0

1       0       1       0

1       1       0       1

 

 

 

 

 

 

 

 

 

 

Clase #11 Suma y multiplicacion de binarios

suma de binarios

 

Para sumar binario es importante saber esto:  0+0=0,   0+1=1,   1+1=10.

para sumas en binario se hace de forma tradicional, solo que se usa las tres condiciones, se empieza a sumar de derecha a izquierda.

EJEMPLO: 

                         110110

                       +111011

                        ------------

                       1110001

 

 

 

Multiplicacion de binarios.



Para multiplicar numeros binario es impoprtante saber esto:   1*1=1,    1*0=0,     0*0=0

para multiplicar numeros binarios se hace de la forma tradicional, de la misma manera que si estuvieramos multiplicando numeros naturales

 

EJEMPLO:

 

                  10

                *10

          --------------

                  00

                10

           -----------

                100 

 

Clase #10 N° binarios

QUE SON LOS NUMEROS BINARIOS

 

 

 

Son números que están dentro del sistema binario de numeración que está constituido por dos cifras 1 y 0, un sistema en el cual se escriben cantidades, códigos, mensajes y otros lenguajes con tan solo dos elementos dentro de la numeración, haciendo que el código se simplifique la comprensión de los sistemas informáticos, pues hará que un elemento tenga un valor unitario o nulo.

El sistema binario de numeración es utilizado con mucha frecuencia y fue el origen de los sistemas informáticos como las calculadoras y las computadoras. Esto se debe a que la simplificación del lenguaje logra un nivel bajo de error pues se basa en dos únicas respuestas por parte del interprete. Es decir, que solo puede haber dos interpretaciones por cada símbolo. Una puerta está abierta o cerrada, nunca puede haber un valor intermedio.

Por ejemplo el valor para 25 en binario es 11001

 

 

 

Al organizar los numeros se elevan a la dos, y se suman para comprobar que este bien el resultado del numero que pasamos a binario